Треугольник

• Треугольник — это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован тремя лучами, выходящими из вершин треугольника и проходящими через две другие вершины.

Внешним углом треугольника является угол, смежный внутреннему углу треугольника:

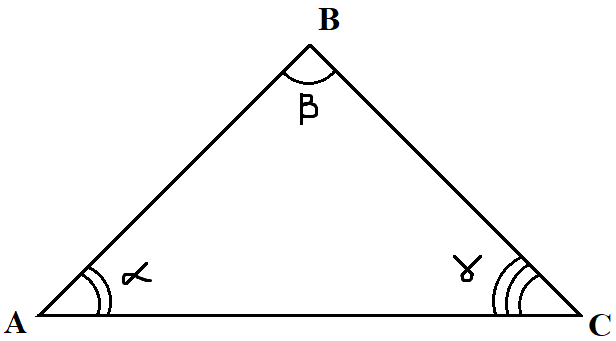
Запомни!

1. Сумма углов треугольника равна 180°
        α + β + γ = 180°
2. Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон:
        AB + BC >AC
        AC + AB >BC
        AC + BC >AB
3. В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.

Медиана, биссектриса, высота

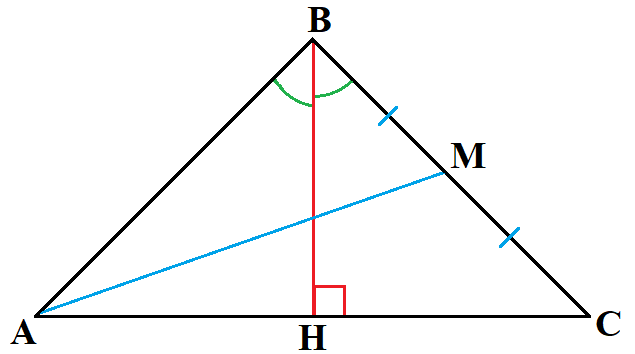
• Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.
  AM – медиана, BM = MC.
• Биссектриса треугольника  — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.
  ∠ AHB = ∠ CHB = 90°
• Высота треугольника  — это перпендикуляр, опущенный из его вершины на противоположную сторону.
  ∠ ABH = ∠ CBH

Средняя линия треугольника

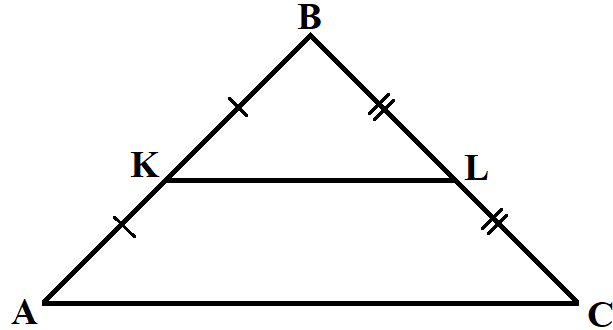
• Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
• Средняя линия параллельна одной из сторон треугольника и равна ее половине.
• AK = KB, BL=LC, KL || AB, KL=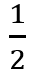AC

Формулы площади треугольника:

• S = 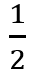a∙h, где a – сторона, h – высота, проведенная к ней.
• S = 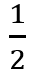a∙b∙sinα, где a, b – стороны, а α – угол между сторонами a и b.

Виды треугольников

Равнобедренный треугольник

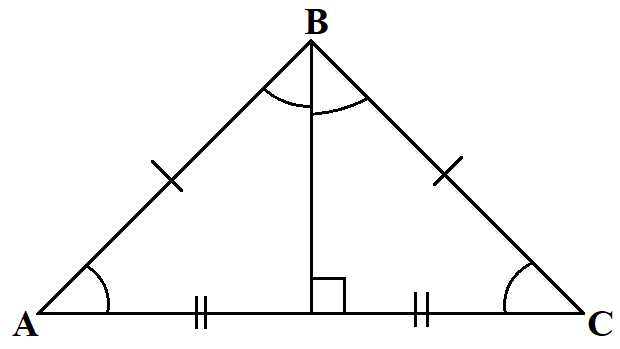
• Две стороны равны — боковые стороны.
• Третья сторона — основание.
• Углы при основании равны.
• В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

Равносторонний треугольник

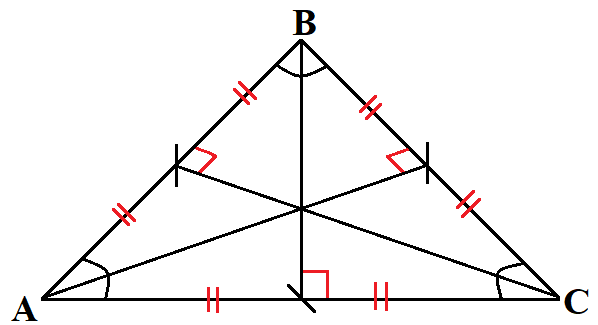
• Все стороны равны
• Все углы равны по 60°.
• Медианы, биссектрисы и высоты совпадают.
• Радиус окружности, вписанной в правильный треугольник со стороной a:
  
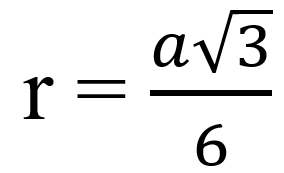
• Радиус окружности, описанной около правильного треугольника со стороной a:
  

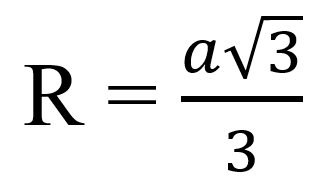
Прямоугольный треугольник

• Один из углов равен 90°.
• Сумма острых углов равна 90°.
• Катет, противолежащий углу в 30°, равен половине гипотенузы. И обратно, если в треугольнике катет в два раза меньше гипотенузы, то напротив него лежит угол в 30°.
• Теорема Пифагора:
  с² = a² + b², с – гипотенуза, a и b – катеты.
• Площадь: S = 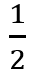a∙b, a и b – катеты.
  
• Высота h прямоугольника треугольника, проведенная к гипотенузе, равна:
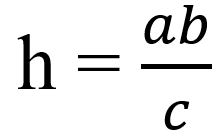  , где a и b – катеты, с – гипотенуза.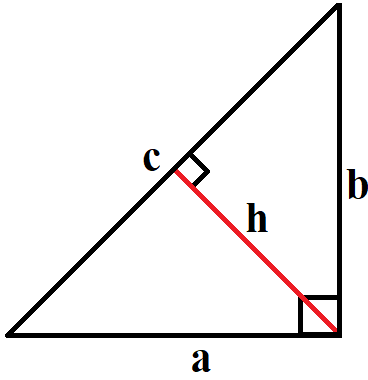
  
• Центр описанной окружности – середина гипотенузы.
• Радиус R описанной окружности есть половина гипотенузы с:
  
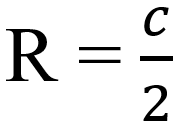
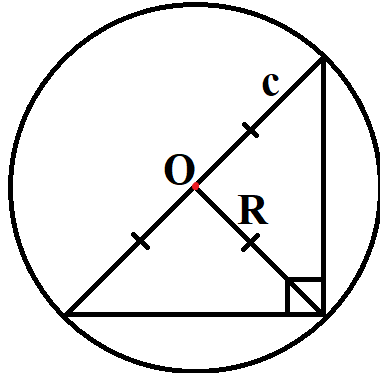
• Медиана, проведенная к гипотенузе, равняется ее половине.
• Радиус r вписанное окружности равен:
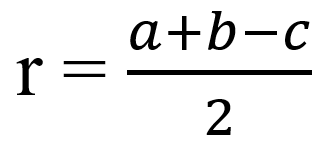  , где a и b – катеты, с – гипотенуза.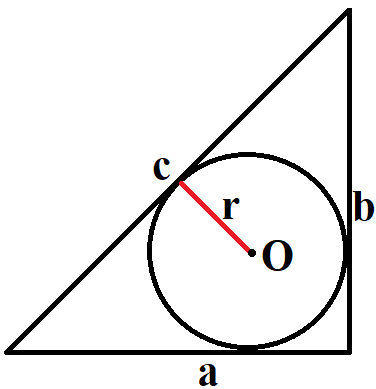
  

Тригонометрические соотношения

• Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
• Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
• Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
• Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащего.

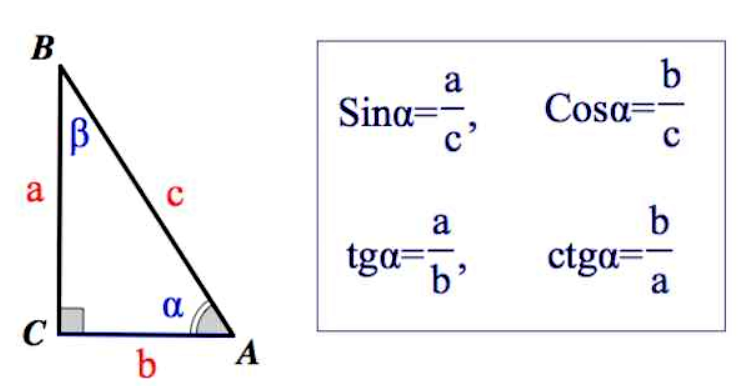
Кроме того:

• sin2(x) + cos2(x) = 1
• tg(x)ctg(x) = 1

Равенство треугольников

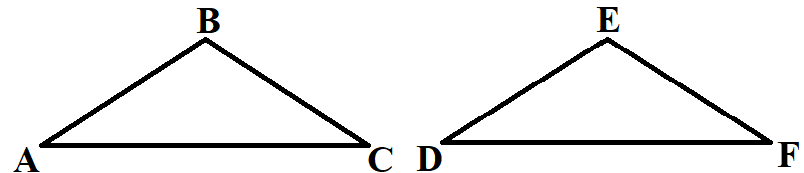
Если ΔAВC и ΔDEF можно совместить наложением, то они являются равными. У равных треугольников равны и их соответствующие элементы.

Первый признак равенства треугольников:

• По двум сторонам и углу между ними.

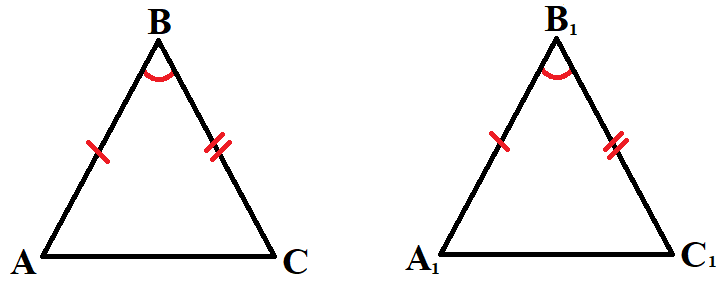
Если AB = A₁B₁, BC = B₁C₁, ∠ABC = ∠A₁B₁C₁, то ΔABC = ΔA₁B₁C₁

Второй признак равенства треугольников:

• По двум углам и стороне прилежащей к ним.

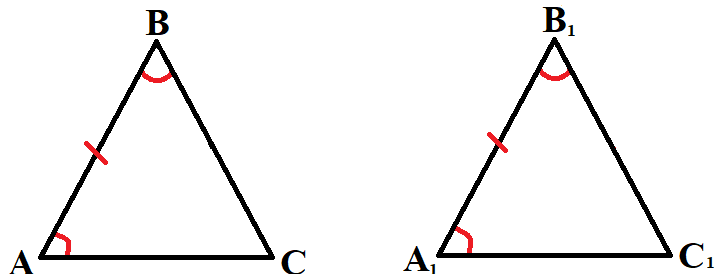
Если AB = A₁B₁, BAC = B₁A₁C₁, ∠ABC = ∠A₁B₁C₁, то ΔABC = ΔA₁B₁C₁

Третий признак равенства треугольников:

• По трём сторонам.

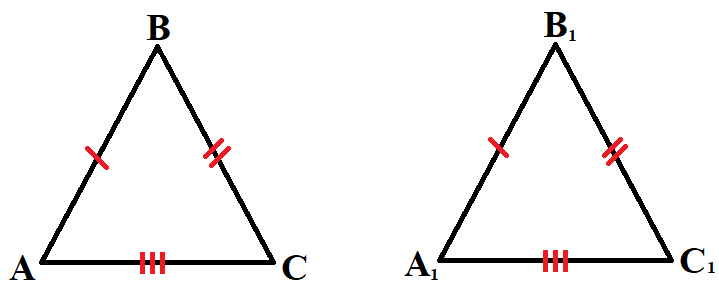
Если AB = A₁B₁, AC = A₁C₁, BC = B₁C₁, то ΔABC = ΔA₁B₁C₁

Подобие треугольников

• Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.

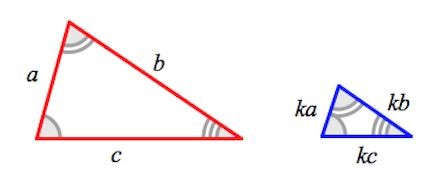
Коэффициент подобия:

Величина, которая равна отношению сходственных сторон треугольников, называется коэффициентом подобия. Коэффициент подобия треугольников обозначается буквой k, k > 0. Таким образом, приведённое выше равенство можно записать в виде:

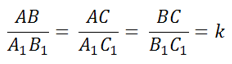
Первый признак подобия треугольников

• Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

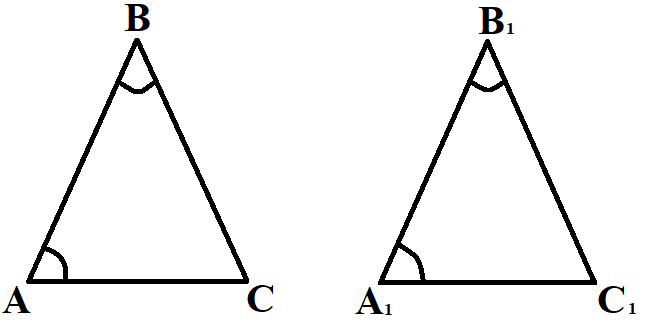
Если ∠A = ∠A₁ и ∠B = ∠B₁, то ΔABC ∼ ΔA₁B₁C₁.

Второй признак подобия треугольников

• Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

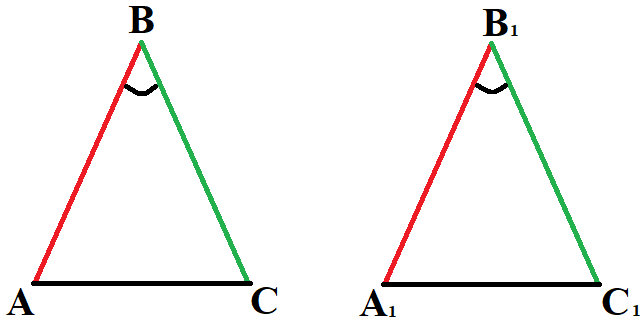
Если ∠B = ∠B₁, 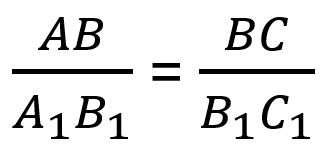, то ΔABC ∼ ΔA₁B₁C₁.

Третий признак подобия треугольников

• Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

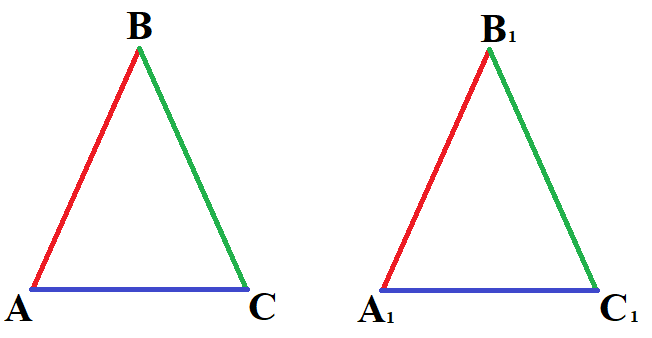
Если 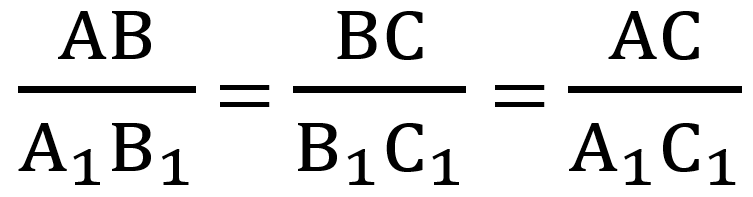, то ΔABC ∼ ΔA₁B₁C₁.

Площади подобных треугольников

Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия