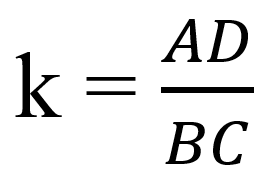Теория
Четырехугольники
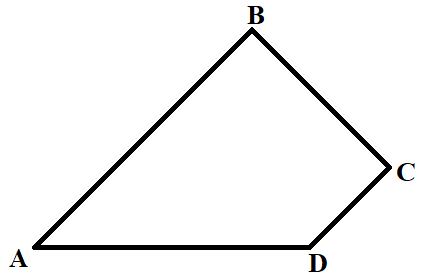
- Четырехугольник – это фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины.
- Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.
- Сумма углов выпуклого четырёхугольника равна 360°:
∠A+∠B+∠C+∠D=360°. - Сумма внутренних углов четырехугольника pавна 360°:
∠A+∠B+∠C+∠D=360°. - Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов:
∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D,
∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. - Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон:
AB< BC+CD+DA, BC < CD+DA+ AB,
CD < BC+ DA+ AB, DA < BC+CD+ AB.
Вписанная в четырехугольник и описанная около четырехугольника окружность
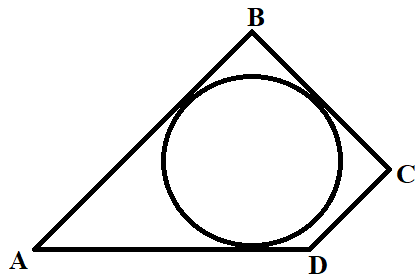
Свойства вписанной в четырехугольник окружности:
- Если четырехугольник описан около окружности, то сумма двух его противолежащих сторон равна сумме двух других его сторон.
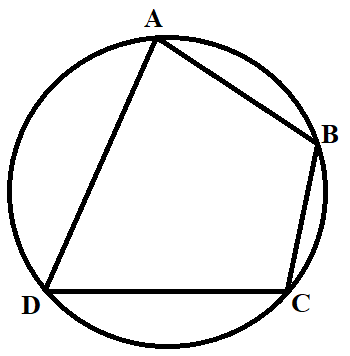
Признаки описанной около четырехугольника окружности:
- Если в четырехугольнике сумма двух его противолежащих сторон равна сумме двух других его сторон, то в четырехугольник можно вписать окружность.
Параллелограмм
- Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны.
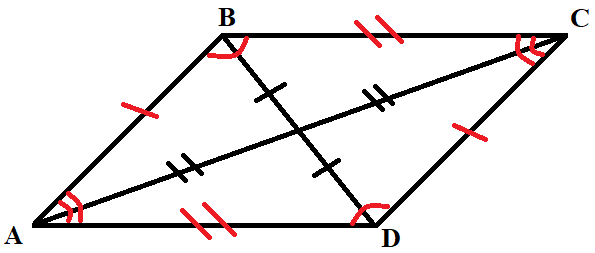
Свойства:
- Противоположные стороны параллелограмма равны:
AB = CD, BC = AD - Противоположные стороны параллелограмма параллельны:
AB || CD, BC || AD - Противоположные углы параллелограмма равны:
∠ABC = ∠CDA, ∠BCD = ∠DAB - Сумма углов прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180° - Каждая диагональ параллелограмма делит его на два равных треугольника.
- Две диагонали делят параллелограмм на две пары равных треугольников.
- Диагонали параллелограмма точкой пересечения делят друг друга пополам.
- Точка пересечения диагоналей называется центром симметрии параллелограмма.
- Параллелограмм имеет две диагонали – длинную – AC и короткую – BD.
- В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
- Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником.
Площадь параллелограмма:
- S = a∙h, где a – основание, h – высота.
Ромб
- Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
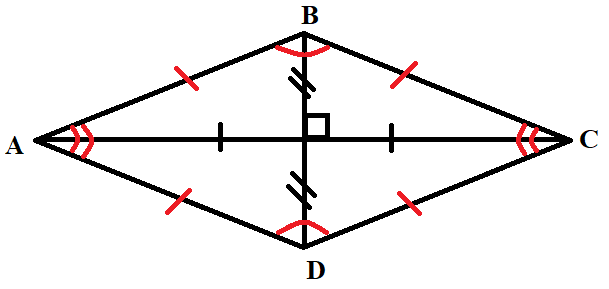
Свойства:
- Имеет все свойства параллелограмма.
- Все стороны равны:
АВ = ВС = СD = AD - Диагонали пересекаются под прямым углом:
AC ┴ BD - Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC - Все высоты равны:
BN = DL = BM = DK - В ромб можно вписать окружность.
- Около ромба нельзя описать окружность.
Площадь ромба:
- S = a∙h, где a – основание, h – высота.
- S =
d1∙d2 , где d1 и d2 – диагонали.
Трапеция
- Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны или трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
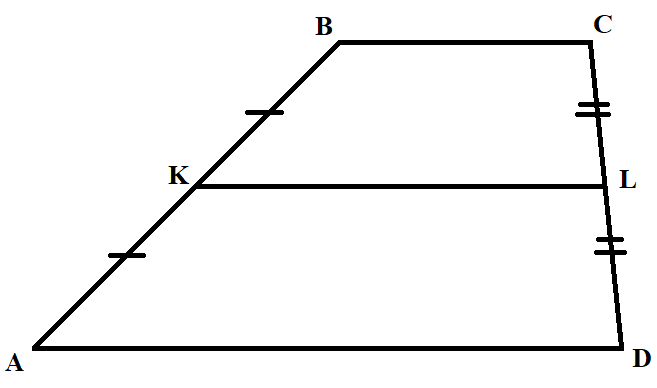
Свойства:
- AD и BC – основания, AB, CD – боковые стороны.
- AD || BC
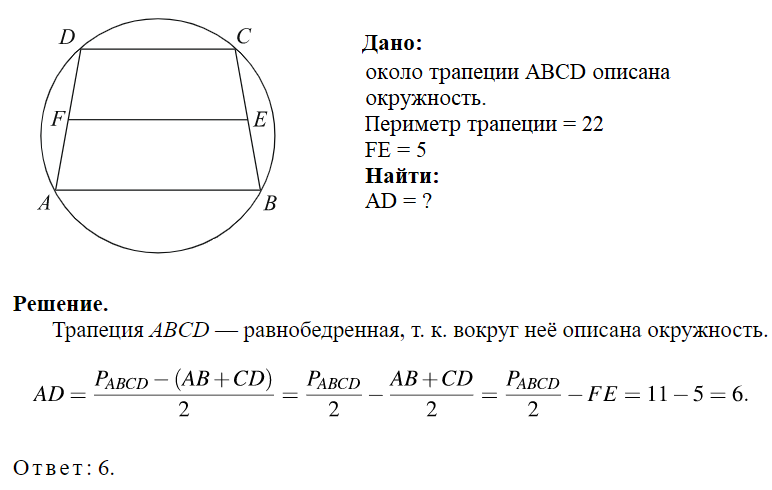
- Если боковые стороны трапеции равны, то такая трапеция будет называться равнобедренной.
- Если у трапеции есть прямые углы при боковой стороне, то такая трапеция называется прямоугольной.
- Если в трапецию можно вписать в окружность, то трапеция равнобедренная
- В трапецию можно вписать окружность, если AD + BC = AB + CD
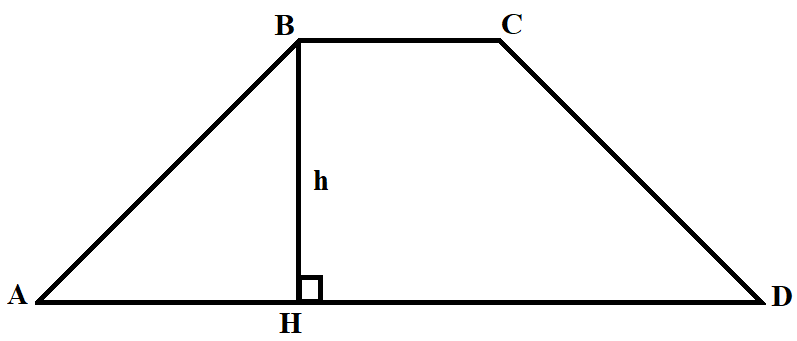
Средняя линия трапеции:
Средняя линия KL – отрезок, соединяющий середины боковых сторон.
- AD || KL и KL || BC
- AK = KB, CL = LD
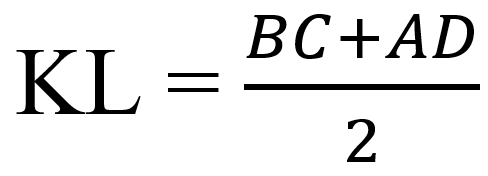
Площадь трапеции:
- S =
∙h = KL∙ h, где h – высота
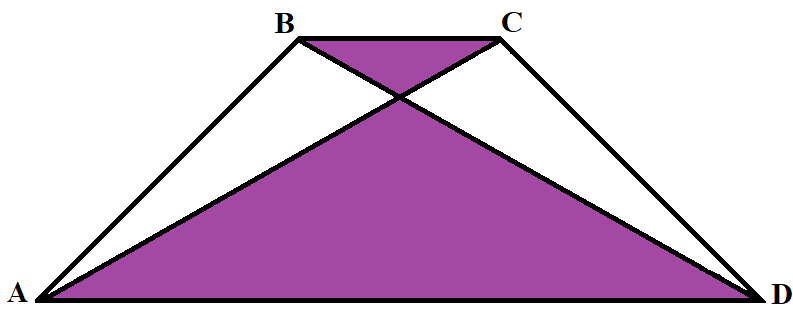
Свойства диагоналей:
- ΔOBC и ΔAOD – образованные диагоналями и основаниями подобны (ΔOBC ∼ ΔAOD)
- Коэффициент подобия
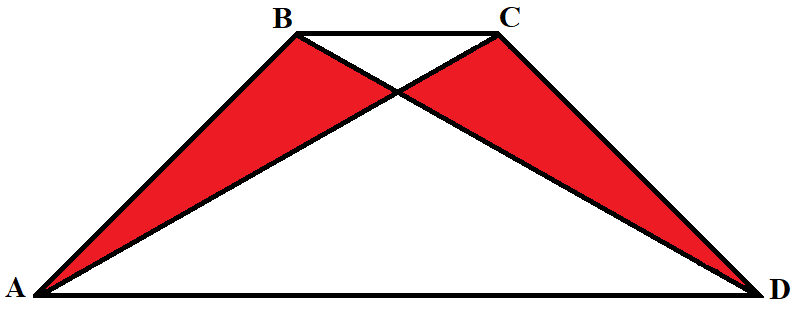
- ΔABO и ΔOCD –образованные диагоналями и боковыми сторонами будут иметь одинаковую площадь (SABO = SOCD)
Равнобедренная трапеция:
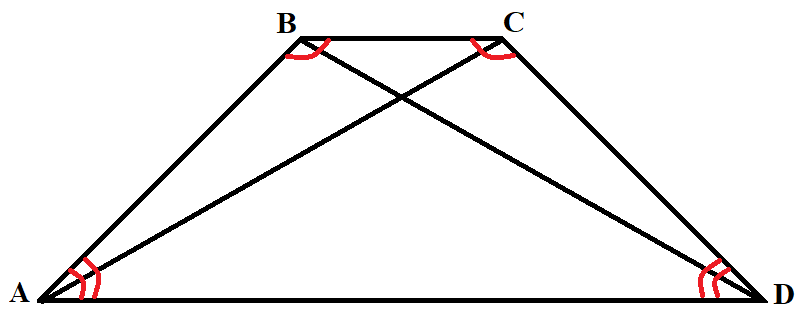
Свойства:
- Боковые стороны равны: AB = CD
- Углы при основании равны: ∠B = ∠C, ∠A = ∠D
- Диагонали равны: AC = BD
Прямоугольная трапеция:
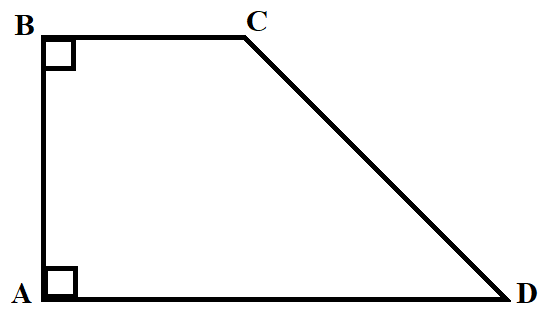
Свойства:
- ∠A = ∠B = 90°
- Высота и боковая сторона трапеции, прилежащая к прямому углу, совпадают.
Правильные многоугольники
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
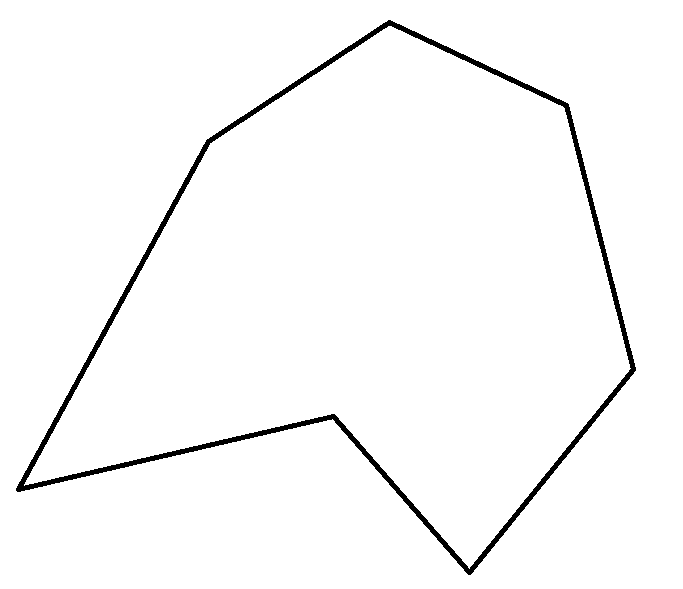
- Правильный многоугольник — это многоугольник, у которого все стороны и углы равны.
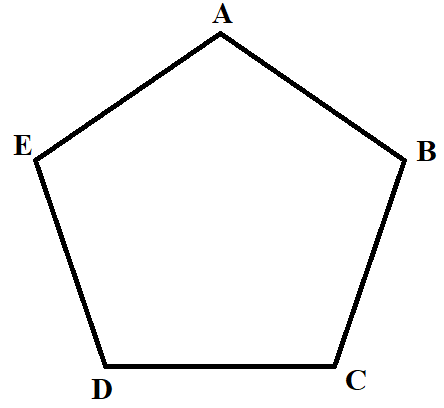
Свойства:
- Все стороны равны:
a1 = a2 = a3 = a4 = ... = an - Все углы равны:
α1 = α2 = α3 = ... = αn-1 = αn - Центр вписанной окружности совпадает c центром описанной окружности, образуя центр многоугольника O
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
- Сумма всех углов n-угольника равна:
180° · (n – 2) - Градусная величина угла n-угольника равна:
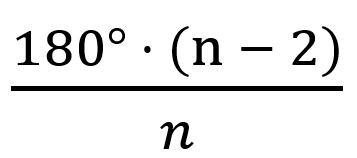
- Около любого правильного n-угольника можно описать окружность
- В любой правильный n-угольник можно вписать окружность
Практика
1. Периметр параллелограмма равен 48 см. Найдите стороны параллелограмма, если разность двух сторон равна 3 см.
Показать решение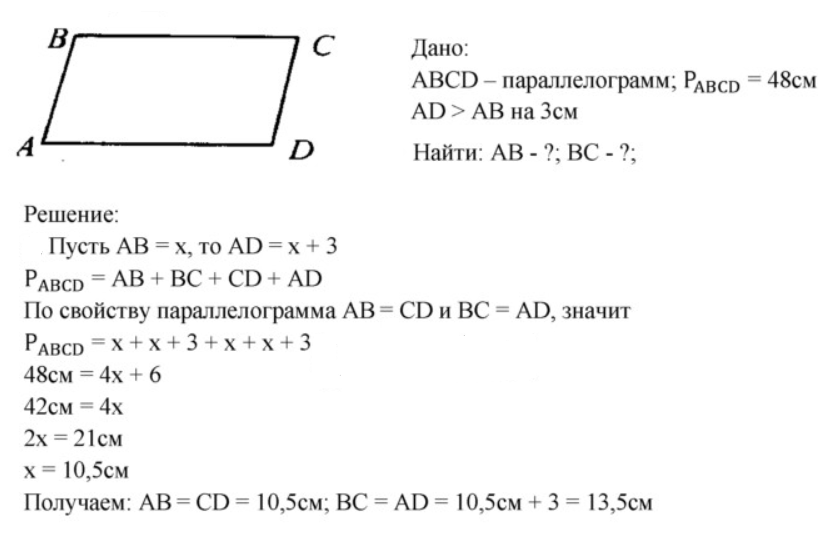
2. Найдите углы параллелограмма ABCD, если: a) ∠A = 84°; б) ∠CAD=16°, ∠ACD = 37°.
Показать решение
3. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.
Показать решение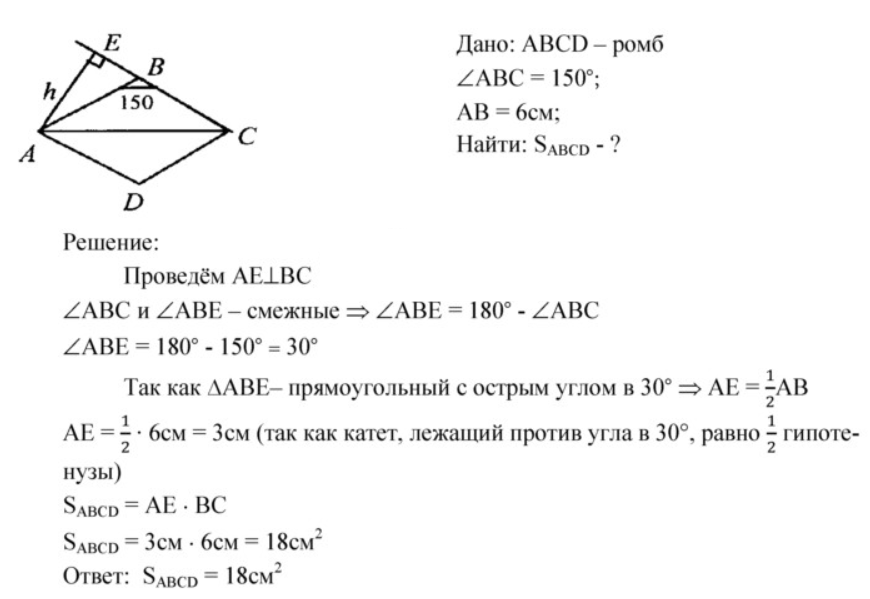
4. Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
Показать решение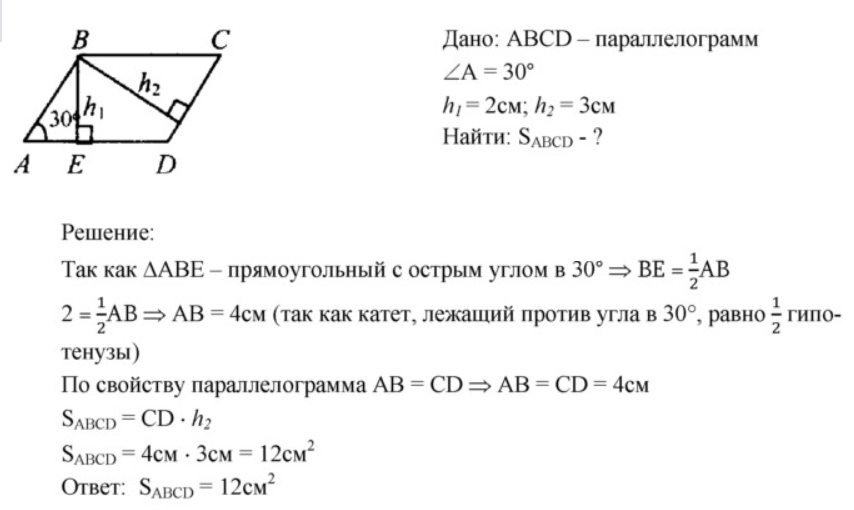
5. Один из углов равнобедренной трапеции равен 68°. Найдите остальные углы трапеции.
Показать решение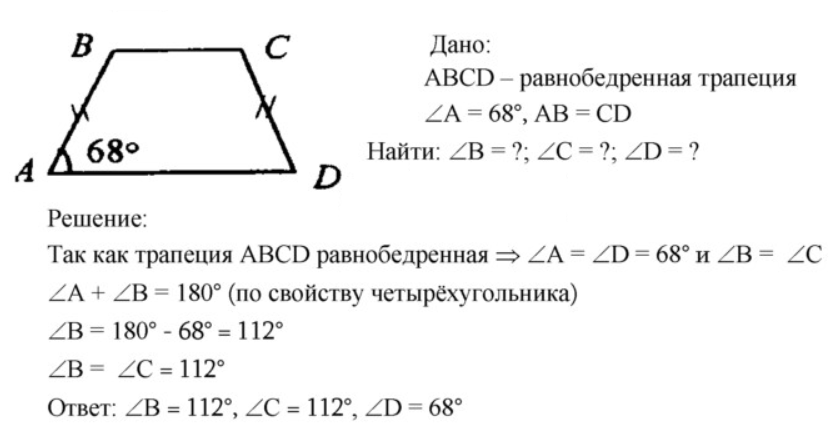
6. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.
Показать решение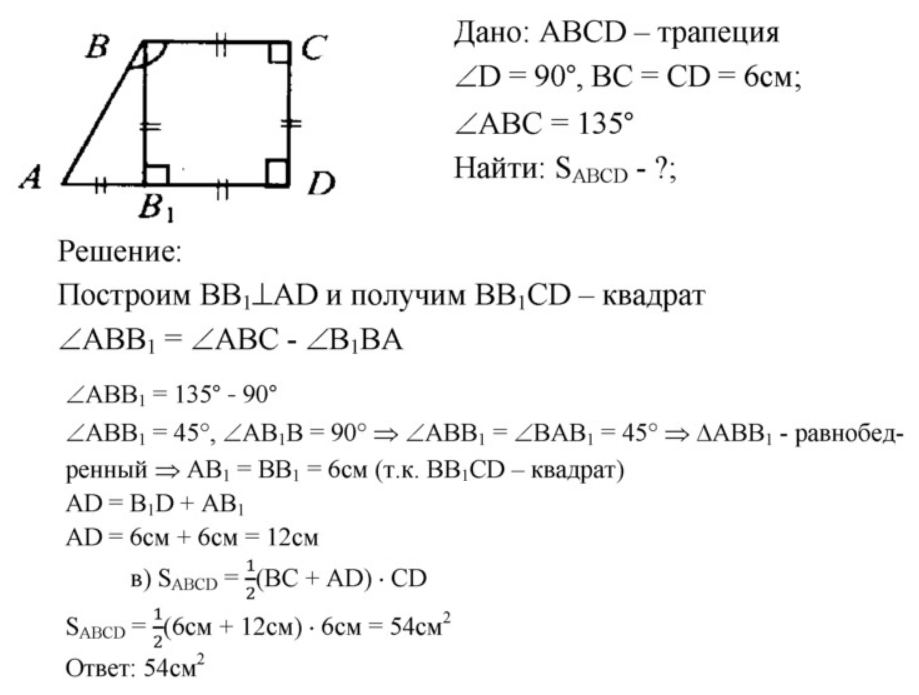
7. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Показать решение
8. ABCDEFGH — правильный восьмиугольник. Найдите угол EFG. Ответ дайте в градусах.
Показать решение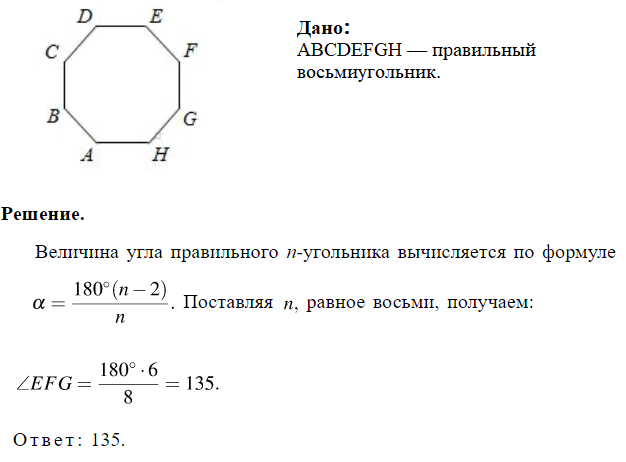
9. В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 8.
Показать решение
10. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Показать решение